This is another one of those where it doesn't look like there's enough information to solve it, but there's clearly only one solution, so there must be!
Consider the case of a pole leaning inside a barrel, such that it rests against both sides and the bottom, forming the three points A, C, and E. These three points and the inside corners of the barrel form two similar right triangles, ABC and CDE.
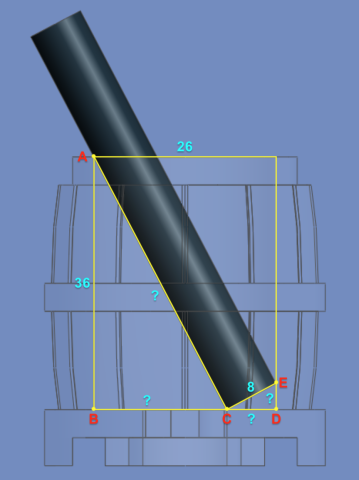
From the known part dimensions, we get the hypotenuse (8) of the smaller triangle and one leg (36) of the larger triangle. We also know that an additional leg from each triangle, BC and CD, add up to 26.
We want to find the missing lengths AC, BC, CD and DE, and by extension, the congruent acute angles at A and C. That will give us the rotation points and angle for the bar. Can we do it?
Consider the case of a pole leaning inside a barrel, such that it rests against both sides and the bottom, forming the three points A, C, and E. These three points and the inside corners of the barrel form two similar right triangles, ABC and CDE.
From the known part dimensions, we get the hypotenuse (8) of the smaller triangle and one leg (36) of the larger triangle. We also know that an additional leg from each triangle, BC and CD, add up to 26.
We want to find the missing lengths AC, BC, CD and DE, and by extension, the congruent acute angles at A and C. That will give us the rotation points and angle for the bar. Can we do it?













