It's puzzle time again!

[N. W. Perry]

This is another one of those where it doesn't look like there's enough information to solve it, but there's clearly only one solution, so there must be!

Consider the case of a pole leaning inside a barrel, such that it rests against both sides and the bottom, forming the three points A, C, and E. These three points and the inside corners of the barrel form two similar right triangles, ABC and CDE.
   
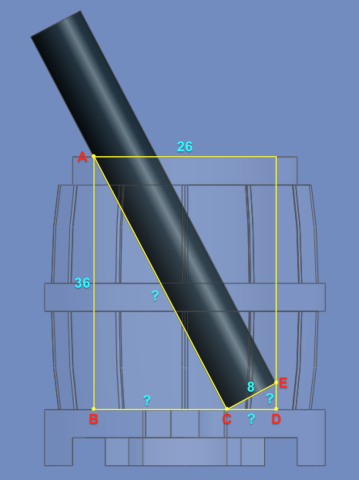
From the known part dimensions, we get the hypotenuse (8) of the smaller triangle and one leg (36) of the larger triangle. We also know that an additional leg from each triangle, BC and CD, add up to 26.

We want to find the missing lengths AC, BC, CD and DE, and by extension, the congruent acute angles at A and C. That will give us the rotation points and angle for the bar. Can we do it?

[Gerald Lasser]

I let GeoGebra do the job and it tells me that the 0 point for 8 - ((26-36 tan (A))/cos(A)) is 27,7222764 degrees

Making BC = 18,91828 LDU

[Milan Vančura]

That's interesting question. Although the initial conditions are easy to formalize, they let to an eq. of degree 4 - or I'm missing something

let set y=|DE| ; l=|BC| ; r=|CD|; S=26; V=36; T=8 - then:

L + R = S  (evident)
R^2 + y^2 = T^2  (Pythagoras theorem)
y/R = L / V  (similar triangles)
                                                            

Another approach is to use analytic geometry: for each point C compute the eq. of bar bottom-right corner point- then, set the x coordinate of this point equal 26. Maybe I try this later but you might be faster

EDIT: This leads to eq. of degree 4 as well. Hmm, strange. Not only because of a need to solve such eq. but from physical POV as well: how we can tell why only one of those 4 solutions is real and other three not?  Looks, I felt into a trap, I can see why this was announced as a puzzle now

[N. W. Perry]

I let GeoGebra do the job and it tells me that the 0 point for 8 - ((26-36 tan (A))/cos(A)) is 27,7222764 degrees

Making BC = 18,91828 LDU

What did you enter into GeoGebra to find this? I sketched it there myself, but I don't know how to enter all of the constraints I need. (Dimensions are different in my sketch because I was dealing with different parts, but the problem is the same.)

[Gerald Lasser]

What did you enter into GeoGebra to find this? I sketched it there myself, but I don't know how to enter all of the constraints I need. (Dimensions are different in my sketch because I was dealing with different parts, but the problem is the same.)

Basically I made a function that shall solve to 0 at the given angle

so given that:
angle ABC = angle CDE
BC+CD = 26

I took:
tan(ABC)= BC/36
BC=36*tan(ABC)

and then

CD= 8*cos(ABC)
26 - 36*tan(ABC) = 8* cos(ABC)

so I made a graph for

f(ABC) = 26 - 36*tan(ABC) - 8* cos(ABC)

then the term  get 0 we have a solution
 
   

[N. W. Perry]

Basically I made a function that shall solve to 0 at the given angle

so given that:
angle ABC = angle CDE
BC+CD = 26

Right, except it's BAC and DCE in the picture, but no matter…

I took:
tan(ABC)= BC/36
BC=36*tan(ABC)

Got it, tan=O/A…

and then

CD= 8*cos(ABC)

And cos=A/H…

26 - 36*tan(ABC) = 8* cos(ABC)

so I made a graph for

f(ABC) = 26 - 36*tan(ABC) - 8* cos(ABC)

Of course, since the two sides are equal, subtract one side from the other to get zero…

then the term  get 0 we have a solution

So the solution is 0.483845377…? How does we get 27.7222764 degrees from that?

Sorry, I'm still slow with the algebra side of it! 

[Gerald Lasser]

So the solution is 0.483845377…? How does we get 27.7222764 degrees from that?

Sorry, I'm still slow with the algebra side of it! 

0.48 is in Radians, i.e. a full circle (360 °) is 2*pi
So 0.48/(2*pi) *360 you get degrees

[N. W. Perry]

0.48 is in Radians, i.e. a full circle (360 °) is 2*pi
So 0.48/(2*pi) *360 you get degrees

D'oh! Of course, radians. Those get me every time.

And of course I tried this angle, and it does appear to be correct!

[Milan Vančura]

D'oh! Of course, radians. Those get me every time.

And of course I tried this angle, and it does appear to be correct!

Sure, it's good to solve the practical problem. But I am really surprised I couldn't find any analytic solution, a clear statement L=f(s,v,b) as I wrote lower. Strange. Such easily-formulated problem leading to so complicated solution?

[Javier Orquera]

Hello: I am not a mathematician but, on my knowledge, the equation in the graph is wrong: you change the sign of 36tan(x); it is -36tan(x) when in reality is +36tan(x)

[N. W. Perry]

Hello: I am not a mathematician but, on my knowledge, the equation in the graph is wrong: you change the sign of 36tan(x); it is -36tan(x) when in reality is +36tan(x)

I haven't figured out the graph equation, either…as far as I can see, it's enough to put f(x) = 26 - 36tan(x) - 8cos(x). But the software will rearrange it as it sees fit, I suppose…