I'm overdue for a math puzzle, I think, so here's one from 10234 Sydney Opera House! I've attached the instructions page I'm working on. I haven't given up yet, but I also haven't figured out the answer, so why not play along?
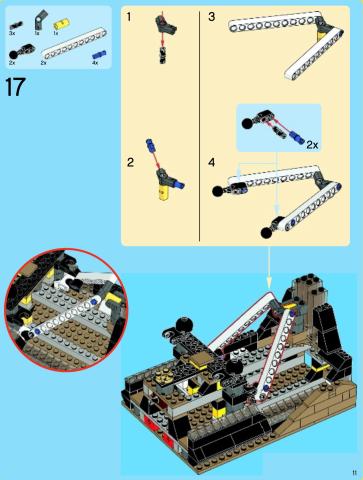
Basically there's a y-shaped yoke with two technic beams attached, each ending in a ball joint. The ball joints are fixed into two sockets that are 200 LDU apart on center.
The beams are 240 LDU long, from the ball center to the pinhole where they attach to the yoke. (The beam/ball assembly is offset in shape, but because it's pinned to the yoke at a fixed angle, we can simplify by measuring from the ball to a point 20 LDU inboard of where the beam attaches to the yoke.)
The yoke assembly can pivot freely with respect to the beams, so their distance apart at the yoke end is variable (but symmetrical). Because they are pinned to a 135-degree connector, their axes of rotation are each fixed at 22.5 degrees off parallel.
The stem of the yoke (yellow cylinder) rests inside a u-shaped bracket. Importantly, the yoke is NOT pinned to the bracket, so it presumably rests against the inner wall of the bracket but can be at a slight angle, as the instructions suggest. If this is so, then it would pivot around the upper tangent point of the cylinder. The inner surface of the bracket is 200 LDU away horizontally from the ball joints, so the pivot point is fixed there. The top surface of the bracket is 170 LDU vertically away from the ball joints, but the pivot point rests at a non-fixed position that's probably a few LDU lower than the top surface.
I've modeled this in GeoGebra, which you can see here. In this model, point A is adjustable vertically, and point B can be rotated to set the angle of the yoke assembly. Point I is the ball joint, and point F' is the simplified connection point of the beam to the yoke, so it needs to be 240 LDU from point I, indicated by the inner edge of the big purple cylinder. (Point G, and the outer edge of the cylinder, represents the actual connection point of the Technic beam.)
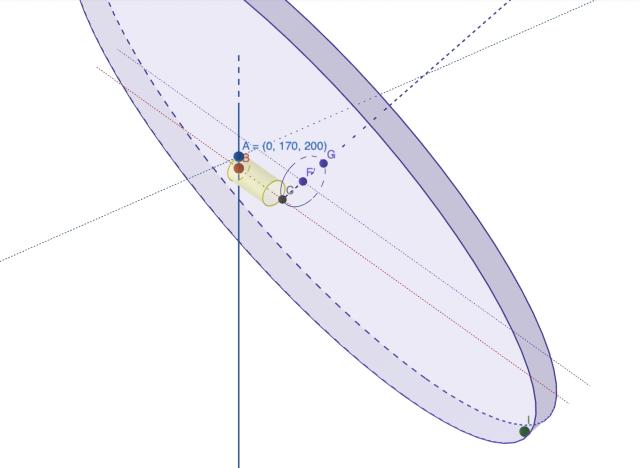
The puzzle is to find the vertical position of A, and the angle of A-B, such that F'-I equals 240 and lies on the inner plane of the big flat cylinder. My hunch is there's only one solution, but that it requires more constraints than GeoGebra can accept. I might be wrong about that, though!
Basically there's a y-shaped yoke with two technic beams attached, each ending in a ball joint. The ball joints are fixed into two sockets that are 200 LDU apart on center.
The beams are 240 LDU long, from the ball center to the pinhole where they attach to the yoke. (The beam/ball assembly is offset in shape, but because it's pinned to the yoke at a fixed angle, we can simplify by measuring from the ball to a point 20 LDU inboard of where the beam attaches to the yoke.)
The yoke assembly can pivot freely with respect to the beams, so their distance apart at the yoke end is variable (but symmetrical). Because they are pinned to a 135-degree connector, their axes of rotation are each fixed at 22.5 degrees off parallel.
The stem of the yoke (yellow cylinder) rests inside a u-shaped bracket. Importantly, the yoke is NOT pinned to the bracket, so it presumably rests against the inner wall of the bracket but can be at a slight angle, as the instructions suggest. If this is so, then it would pivot around the upper tangent point of the cylinder. The inner surface of the bracket is 200 LDU away horizontally from the ball joints, so the pivot point is fixed there. The top surface of the bracket is 170 LDU vertically away from the ball joints, but the pivot point rests at a non-fixed position that's probably a few LDU lower than the top surface.
I've modeled this in GeoGebra, which you can see here. In this model, point A is adjustable vertically, and point B can be rotated to set the angle of the yoke assembly. Point I is the ball joint, and point F' is the simplified connection point of the beam to the yoke, so it needs to be 240 LDU from point I, indicated by the inner edge of the big purple cylinder. (Point G, and the outer edge of the cylinder, represents the actual connection point of the Technic beam.)
The puzzle is to find the vertical position of A, and the angle of A-B, such that F'-I equals 240 and lies on the inner plane of the big flat cylinder. My hunch is there's only one solution, but that it requires more constraints than GeoGebra can accept. I might be wrong about that, though!




