I feel like I'm under-using LDCad's advanced rotation capabilities. But instead of a question, I think it's easier to just give an example—and sort of a challenge. 
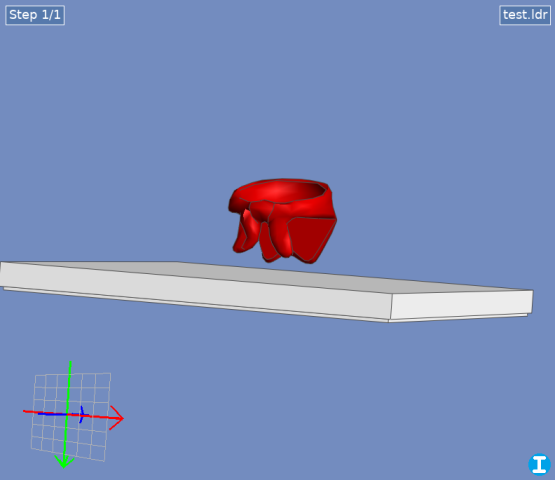
In the attached test file I have an oddly-shaped piece that I want to rest on the ground, here represented by a nice big tile. This part has four lower extremities, all with different y-values, and to be realistic it would need to rest against the lowest three of them. What's the best way to do this using LDCad?
 test.ldr (Size: 173 bytes / Downloads: 2)
test.ldr (Size: 173 bytes / Downloads: 2)
Here's how I would approach it:
Is there a better way? How would you approach this problem?
(Can't attach the .lua file for the angle script, but here it is

In the attached test file I have an oddly-shaped piece that I want to rest on the ground, here represented by a nice big tile. This part has four lower extremities, all with different y-values, and to be realistic it would need to rest against the lowest three of them. What's the best way to do this using LDCad?
 test.ldr (Size: 173 bytes / Downloads: 2)
test.ldr (Size: 173 bytes / Downloads: 2)
Here's how I would approach it:
- Find the lowest point and set it as the rotation center. You could use a helper part or a marker, but how do you find the point itself? Easiest way would be if you could directly select the vertex—LDCad can't do this, but LDPE can.
- Find the next lowest point the same way, then using more helper parts and some trigonometry (or the handy, but unofficial, right angle calc script), rotate the part so this hits the ground.
- For the final rotation, select the third low point, and rotate around a vector formed by the first two points. LDCad does allow custom vector rotation—but how do I find the vector and enter it into the rotation dialog?
Is there a better way? How would you approach this problem?
(Can't attach the .lua file for the angle script, but here it is

Code:
function onRun()
local sel=ldc.selection()
if sel:getRefCount()<3 then
return
end
local a=sel:getRef(1):getPos()
local b=sel:getRef(2):getPos()
local c=sel:getRef(3):getPos()
local ba=a-b
local bc=c-b
local n=bc:getCross(ba)
n:normalize()
local bb1=n:getSignedAngle(ba, bc)
local bb2=math.deg(math.acos(bc:getLength()/ba:getLength()))
local angle=-(bb1-bb2)
ldc.setClipboardText(angle)
ldc.dialog.runMessage(angle)
end
function register()
local macro=ldc.macro('Right angle rotation calc')
macro:setEvent('run', 'onRun')
end
register()





