There's another way to do this, by finding the intersection of two circles. This might be handy if you need to do it in a program that doesn't have LDCad's triangle calculation feature (or if, as I did, you forgot that feature exists and spent an hour figuring it out for yourself and are feeling all clever about it).

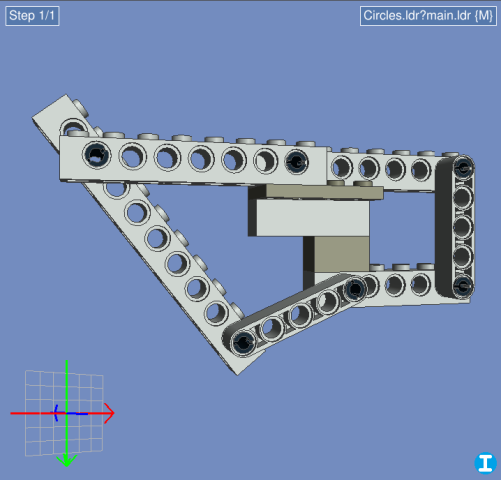
To illustrate this, I whipped up the same model in LDCad. I've added some circular paths to show the circles, but you actually don't need them. All you have to do now is calculate the intersection of the two circles (highlighted in yellow).
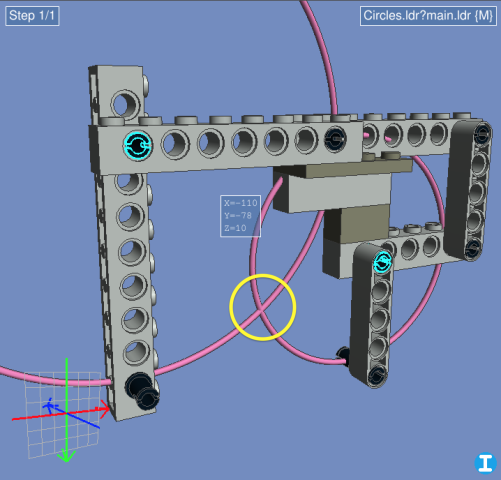
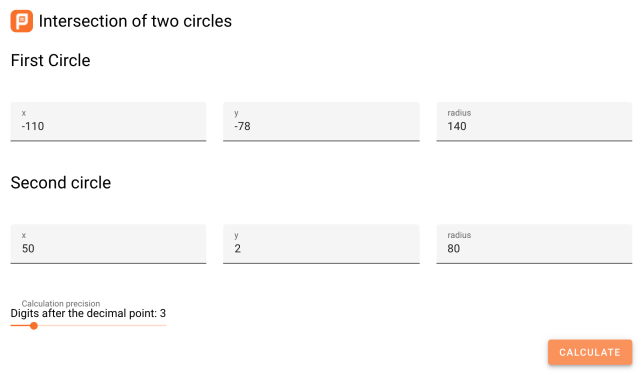
It turns out that's pretty simple math (for a computer) if you know the X,Y position of the center of each circle (we do: the selected pins) and its radius (we can find out: by using LDCad's selection info, or in this case just counting studs). You can look up the mathematical formula if you want, but it's much quicker to use an online calculator—I found
this one, which works perfectly. So let's enter the values we know: we need the X and Y coordinates of the selected pins (we can ignore the Z), and the radii (distance to the end pins: 140 and 80)
And the result, complete with a little graph of the two circles:
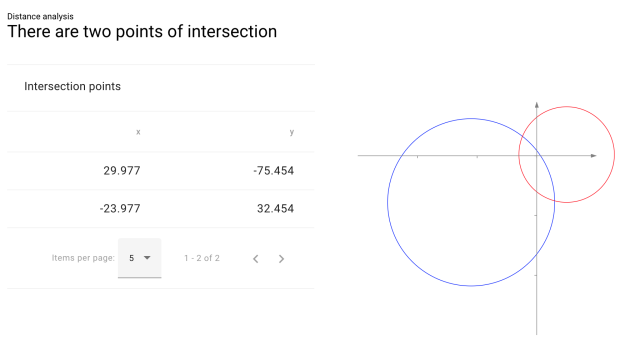 (Note that the graph is a mirror image of the circles in our project, because of the opposite orientation of LDraw's Y axis. But the numbers themselves are correct.)
(Note that the graph is a mirror image of the circles in our project, because of the opposite orientation of LDraw's Y axis. But the numbers themselves are correct.) Of the two intersections found, choose the one that you want to use—in this case it's the second one. Create a new helper part and place it at those X,Y coordinates, then use Selection Info (okay, I guess you still need LDCad for this…) to find the rotation angle you need:
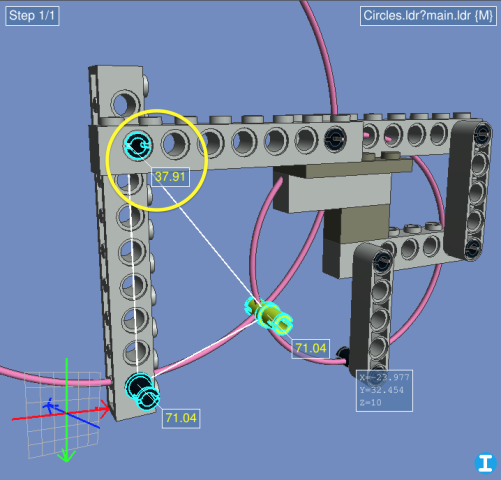
Repeat for the other beam, apply the rotations to both parts, and you're done!
 CalculateAngles.png (Size: 25.41 KB / Downloads: 268)
CalculateAngles.png (Size: 25.41 KB / Downloads: 268)
 CalculateAngles.png (Size: 25.41 KB / Downloads: 268)
CalculateAngles.png (Size: 25.41 KB / Downloads: 268)















