Mm…I couldn't get that method to compute, for some reason.
What did work, though, was to apply the scale factor to both the X and Y directions of the assembly. That makes sense, because…
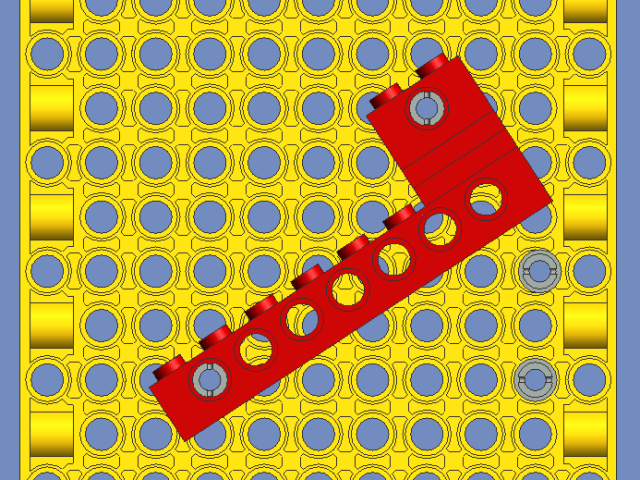
The rotation point and the connection point (the hole in the 1x2 brick) form the hypotenuse of a right triangle. Its length is ~126.49, and I need to stretch it to ~128.06, giving the scale factor of 1.01242. Since the ratio of the sides of a triangle remain the same as long as the angles don't change, then if I want to transform my assembly in the X direction using that same scale factor, I have to apply it in Y as well, to keep the proportions equal.
So after entering 1.01242 into both the X and Y boxes, my hypotenuse now measures 128.06, and I can just apply the rotation shown (32.91°), because again, the angles in my triangle stay the same.
Now, what if I want to stretch my assembly only in the X direction, as originally planned? (Don't ask why—I guess I figured the distortion would be less visually apparent that way.) Well, I know I want my hypotenuse to be 128.06, and since I'm not changing the Y dimension, I know that the short side of my triangle remains at 40 (the vertical distance between the holes in the 1x2 and 1x8 bricks). And since it's a right triangle, I know I have an angle of 90°—and knowing 2 sides plus 1 angle is enough to calculate a whole triangle!
I can either algebraically solve the Pythagorean theorem for b, or just plug the values into my favorite online triangle calculator.
Turns out, my third side needs to be 121.6625; it's currently 120, so that's a scale factor of 1.01379. Enter that into the X matrix, use Selection Info to get the new rotation value (because I changed the ratio of my triangle sides, therefore the angles changed as well), apply that to the assembly—now it fits!
Sorry to ask my question, only to answer myself right away!
I was actually stumped, but for some reason posting these puzzlers here helps me think them through…and maybe will help someone else later on. And it's worth noting that, as usual, my answer lies in the fact that you can solve any triangle if you know at least one side, plus any other 2 of the sides or angles.
What did work, though, was to apply the scale factor to both the X and Y directions of the assembly. That makes sense, because…
The rotation point and the connection point (the hole in the 1x2 brick) form the hypotenuse of a right triangle. Its length is ~126.49, and I need to stretch it to ~128.06, giving the scale factor of 1.01242. Since the ratio of the sides of a triangle remain the same as long as the angles don't change, then if I want to transform my assembly in the X direction using that same scale factor, I have to apply it in Y as well, to keep the proportions equal.
So after entering 1.01242 into both the X and Y boxes, my hypotenuse now measures 128.06, and I can just apply the rotation shown (32.91°), because again, the angles in my triangle stay the same.
Now, what if I want to stretch my assembly only in the X direction, as originally planned? (Don't ask why—I guess I figured the distortion would be less visually apparent that way.) Well, I know I want my hypotenuse to be 128.06, and since I'm not changing the Y dimension, I know that the short side of my triangle remains at 40 (the vertical distance between the holes in the 1x2 and 1x8 bricks). And since it's a right triangle, I know I have an angle of 90°—and knowing 2 sides plus 1 angle is enough to calculate a whole triangle!
I can either algebraically solve the Pythagorean theorem for b, or just plug the values into my favorite online triangle calculator.
Turns out, my third side needs to be 121.6625; it's currently 120, so that's a scale factor of 1.01379. Enter that into the X matrix, use Selection Info to get the new rotation value (because I changed the ratio of my triangle sides, therefore the angles changed as well), apply that to the assembly—now it fits!Sorry to ask my question, only to answer myself right away!
I was actually stumped, but for some reason posting these puzzlers here helps me think them through…and maybe will help someone else later on. And it's worth noting that, as usual, my answer lies in the fact that you can solve any triangle if you know at least one side, plus any other 2 of the sides or angles.